HashMap
HashMap有数组+单向链表/红黑树组成,他在数组大于DEFAULT_INITIAL_CAPACITY(2^4)*DEFAULT_LOAD_FACTOR(0.75f)时进行扩容,最大扩展MAXIMUM_CAPACITY(2^30)大小,而链表大于TREEIFY_THRESHOLD(8)时将链表转化为红黑树。
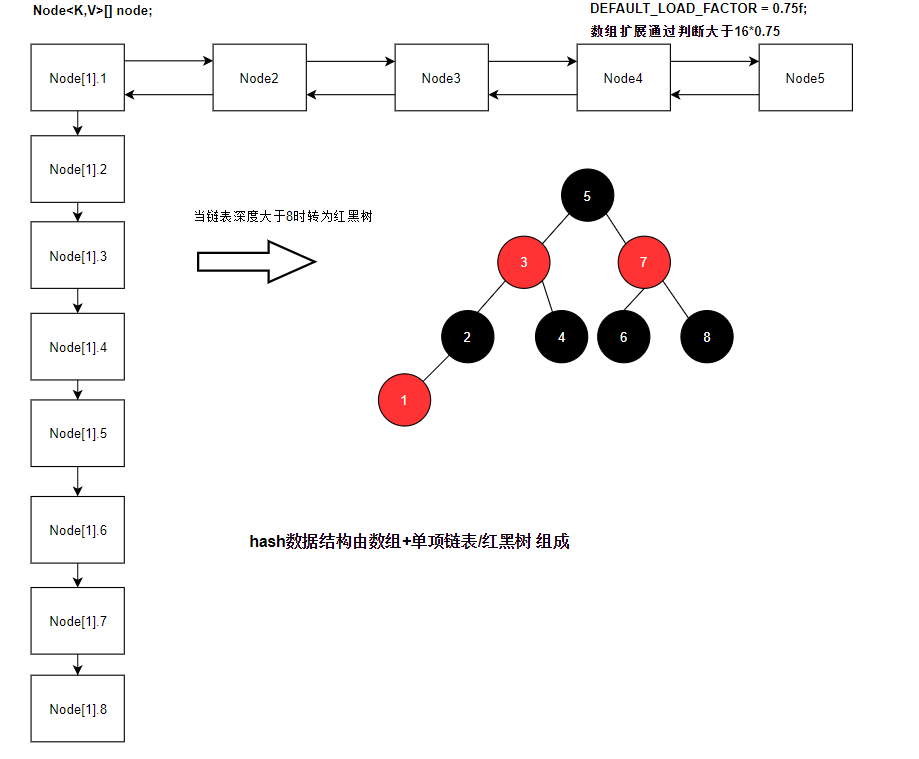
HashMap初始化参数
/**
* The default initial capacity - MUST be a power of two.
* hashmap的默认容量 16
*/
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
/**
* The maximum capacity, used if a higher value is implicitly specified
* by either of the constructors with arguments.
* MUST be a power of two <= 1<<30.最大容量 2^30
*/
static final int MAXIMUM_CAPACITY = 1 << 30;
/**
* 默认加载因子 可通过初始化时进行修改
* The load factor used when none specified in constructor.
*/
static final float DEFAULT_LOAD_FACTOR = 0.75f;
/**
* The bin count threshold for using a tree rather than list for a
* bin. Bins are converted to trees when adding an element to a
* bin with at least this many nodes. The value must be greater
* than 2 and should be at least 8 to mesh with assumptions in
* tree removal about conversion back to plain bins upon
* shrinkage. 链表大于该值时树化 必须是2的倍数
*/
static final int TREEIFY_THRESHOLD = 8;
/**
* The bin count threshold for untreeifying a (split) bin during a
* resize operation. Should be less than TREEIFY_THRESHOLD, and at
* most 6 to mesh with shrinkage detection under removal.
* 小于该值时反树化
*/
static final int UNTREEIFY_THRESHOLD = 6;
/**
* The smallest table capacity for which bins may be treeified.
* (Otherwise the table is resized if too many nodes in a bin.)
* Should be at least 4 * TREEIFY_THRESHOLD to avoid conflicts
* between resizing and treeification thresholds.
* 最小树形化容量阈值:即 当哈希表中的容量 > 该值时,才允许树化,否则直接扩容
*/
static final int MIN_TREEIFY_CAPACITY = 64;
/**
* hashtable 数组
*
*/
transient Node<K,V>[] table;
/**
* The number of key-value mappings contained in this map.
* hashmap大小
*/
transient int size;
/**
* The next size value at which to resize (capacity * load factor).
*
* @serial
*/
// (The javadoc description is true upon serialization.
// Additionally, if the table array has not been allocated, this
// field holds the initial array capacity, or zero signifying
// DEFAULT_INITIAL_CAPACITY.)
int threshold;
/**
* The load factor for the hash table.
* 加载因子
* @serial
*/
final float loadFactor;
// 该构造方法可以初始化容量和加载因子大小
// public HashMap(int initialCapacity, float loadFactor)
链表
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
}
//继承自Node<K,V>
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent; // red-black tree links
TreeNode<K,V> left;
TreeNode<K,V> right;
TreeNode<K,V> prev; // needed to unlink next upon deletion
boolean red;//默认新结点都是红色 红色对红黑树影响最小
TreeNode(int hash, K key, V val, Node<K,V> next) {
super(hash, key, val, next);
}
/**
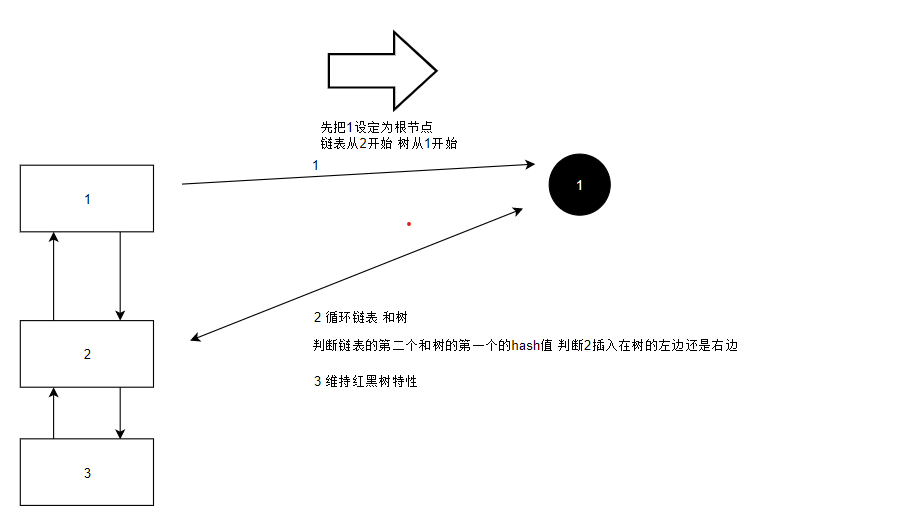
*链表树化
* Forms tree of the nodes linked from this node.
* @return root of tree
*/
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
//x从根节点开始 next 当前节点的下一个节点
for (TreeNode<K,V> x = this, next; x != null; x = next) {//遍历链表
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
if (root == null) {
x.parent = null; //根节点的父节点为null
x.red = false; //根节点变色
root = x;//x为根节点
}
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
//从根节点开始遍历,
//直到找到该节点在树中的位置进行插入
for (TreeNode<K,V> p = root;;) {
int dir, ph;//
K pk = p.key;
//把链表第一个节点设定为根节点
//用根节点循环和链表的下一个比较
//判断当前节点是否大于上一个节点的hash值
if ((ph = p.hash) > h)
dir = -1; //小于0为左子树
else if (ph < h)
dir = 1; //大于0右子树
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) //相等的话
dir = tieBreakOrder(k, pk);//再次比较
TreeNode<K,V> xp = p;//当前节点
if ((p = (dir <= 0) ? p.left : p.right) == null) {//判断左子树或右子树是否为null
x.parent = xp;//当前链表的节点的父节点指向树中该节点对应的树节点
if (dir <= 0)
xp.left = x;
else
xp.right = x;
root = balanceInsertion(root, x);//重新平衡树节点
break;
}
}
}
}
moveRootToFront(tab, root);
}
/**
* Returns a list of non-TreeNodes replacing those linked from
* this node. 反树化 红黑树转化为链表
*/
final Node<K,V> untreeify(HashMap<K,V> map) {
Node<K,V> hd = null, tl = null;
for (Node<K,V> q = this; q != null; q = q.next) {
Node<K,V> p = map.replacementNode(q, null);
if (tl == null)
hd = p;
else
tl.next = p;
tl = p;
}
return hd;
}
/**
* Tree version of putVal.
*/
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
Class<?> kc = null;
boolean searched = false;
TreeNode<K,V> root = (parent != null) ? root() : this;
for (TreeNode<K,V> p = root;;) {
int dir, ph; K pk;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
dir = tieBreakOrder(k, pk);
}
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
Node<K,V> xpn = xp.next;
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
if (dir <= 0)
xp.left = x;
else
xp.right = x;
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode<K,V>)xpn).prev = x;
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}
/**
* Removes the given node, that must be present before this call.
* This is messier than typical red-black deletion code because we
* cannot swap the contents of an interior node with a leaf
* successor that is pinned by "next" pointers that are accessible
* independently during traversal. So instead we swap the tree
* linkages. If the current tree appears to have too few nodes,
* the bin is converted back to a plain bin. (The test triggers
* somewhere between 2 and 6 nodes, depending on tree structure).
*/
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
boolean movable) {
int n;
if (tab == null || (n = tab.length) == 0)
return;
int index = (n - 1) & hash;
TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;
if (pred == null)
tab[index] = first = succ;
else
pred.next = succ;
if (succ != null)
succ.prev = pred;
if (first == null)
return;
if (root.parent != null)
root = root.root();
if (root == null || root.right == null ||
(rl = root.left) == null || rl.left == null) {
tab[index] = first.untreeify(map); // too small
return;
}
TreeNode<K,V> p = this, pl = left, pr = right, replacement;
if (pl != null && pr != null) {
TreeNode<K,V> s = pr, sl;
while ((sl = s.left) != null) // find successor
s = sl;
boolean c = s.red; s.red = p.red; p.red = c; // swap colors
TreeNode<K,V> sr = s.right;
TreeNode<K,V> pp = p.parent;
if (s == pr) { // p was s's direct parent
p.parent = s;
s.right = p;
}
else {
TreeNode<K,V> sp = s.parent;
if ((p.parent = sp) != null) {
if (s == sp.left)
sp.left = p;
else
sp.right = p;
}
if ((s.right = pr) != null)
pr.parent = s;
}
p.left = null;
if ((p.right = sr) != null)
sr.parent = p;
if ((s.left = pl) != null)
pl.parent = s;
if ((s.parent = pp) == null)
root = s;
else if (p == pp.left)
pp.left = s;
else
pp.right = s;
if (sr != null)
replacement = sr;
else
replacement = p;
}
else if (pl != null)
replacement = pl;
else if (pr != null)
replacement = pr;
else
replacement = p;
if (replacement != p) {
TreeNode<K,V> pp = replacement.parent = p.parent;
if (pp == null)
root = replacement;
else if (p == pp.left)
pp.left = replacement;
else
pp.right = replacement;
p.left = p.right = p.parent = null;
}
TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);
if (replacement == p) { // detach
TreeNode<K,V> pp = p.parent;
p.parent = null;
if (pp != null) {
if (p == pp.left)
pp.left = null;
else if (p == pp.right)
pp.right = null;
}
}
if (movable)
moveRootToFront(tab, r);
}
/** ------------------------------------------------------------
*Red-black tree methods, all adapted from CLR 左旋
* p 当前节点 root 根节点
* r 右子树 rl 右子树的左子树 pp 当前节点的父节点
*/
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> r, pp, rl;
if (p != null && (r = p.right) != null) {//判断当前节点和右子节点非空
if ((rl = p.right = r.left) != null)//右子树的左子树不等于null
rl.parent = p; //rl的父节点指向p
if ((pp = r.parent = p.parent) == null) //p的父节点等于空 说明当前节点为根节点
(root = r).red = false;//右子树变成根节点 变色
else if (pp.left == p)//当前节点是其父节点的左子树
pp.left = r; //左旋后 p的父节点的左子树变成p的右子树
else
pp.right = r;//左旋后 p的父节点的右子树变成p的右子树
r.left = p; //左旋后r的左子树是p
p.parent = r;//p的父节点是r
}
return root;
}
//右旋同理
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> l, pp, lr;
if (p != null && (l = p.left) != null) {
if ((lr = p.left = l.right) != null)
lr.parent = p;
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}
//树维持平衡
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
x.red = true;//新插入的节点一定是红色
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) { //向上遍历直至根节点
if ((xp = x.parent) == null) {//父节点是null,说明x是根节点 变黑色 红黑树情况1
x.red = false;
return x;
}
else if (!xp.red || (xpp = xp.parent) == null)//父节点是黑色或祖父节点是null 红黑树情况2
return root;
if (xp == (xppl = xpp.left)) {//父节点是祖父节点的左节点
if ((xppr = xpp.right) != null && xppr.red) {//叔叔节点不为空且是红色 红黑树情况3
xppr.red = false;// 叔叔节点变色
xp.red = false; //父节点变色
xpp.red = true;// 祖父节点变色
x = xpp; // 指向他的祖父节点 一直向上遍历直到根节点
}
else {//LR型 先按父节点左旋 再祖父节点右旋
if (x == xp.right) { //如果是父节点的右节点 情况4?
root = rotateLeft(root, x = xp);//先进行左旋
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {//父节点是祖父节点的左节点 父节点不是null 情况5?
xp.red = false; //父节点黑色
if (xpp != null) { //父节点是祖父节点的左节点 父节点不是null 祖父节点不是null
xpp.red = true; //祖父节点变为红色
root = rotateRight(root, xpp);//右旋
}
}
}
}
else { //父节点是祖父节点的右节点
if (xppl != null && xppl.red) { //叔叔节点不为空且是红色 变色
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else { //RL型 先以父节点右旋,再以祖父节点左旋
if (x == xp.left) {//父节点是祖父节点的右节点 且当前节点是父节点的左子树 父节点右旋
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) { //祖父节点左旋
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root,
TreeNode<K,V> x) {
for (TreeNode<K,V> xp, xpl, xpr;;) {
if (x == null || x == root)
return root;
else if ((xp = x.parent) == null) {
x.red = false;
return x;
}
else if (x.red) {
x.red = false;
return root;
}
else if ((xpl = xp.left) == x) {
if ((xpr = xp.right) != null && xpr.red) {
xpr.red = false;
xp.red = true;
root = rotateLeft(root, xp);
xpr = (xp = x.parent) == null ? null : xp.right;
}
if (xpr == null)
x = xp;
else {
TreeNode<K,V> sl = xpr.left, sr = xpr.right;
if ((sr == null || !sr.red) &&
(sl == null || !sl.red)) {
xpr.red = true;
x = xp;
}
else {
if (sr == null || !sr.red) {
if (sl != null)
sl.red = false;
xpr.red = true;
root = rotateRight(root, xpr);
xpr = (xp = x.parent) == null ?
null : xp.right;
}
if (xpr != null) {
xpr.red = (xp == null) ? false : xp.red;
if ((sr = xpr.right) != null)
sr.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateLeft(root, xp);
}
x = root;
}
}
}
else { // symmetric
if (xpl != null && xpl.red) {
xpl.red = false;
xp.red = true;
root = rotateRight(root, xp);
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl == null)
x = xp;
else {
TreeNode<K,V> sl = xpl.left, sr = xpl.right;
if ((sl == null || !sl.red) &&
(sr == null || !sr.red)) {
xpl.red = true;
x = xp;
}
else {
if (sl == null || !sl.red) {
if (sr != null)
sr.red = false;
xpl.red = true;
root = rotateLeft(root, xpl);
xpl = (xp = x.parent) == null ?
null : xp.left;
}
if (xpl != null) {
xpl.red = (xp == null) ? false : xp.red;
if ((sl = xpl.left) != null)
sl.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateRight(root, xp);
}
x = root;
}
}
}
}
}
}
HashMap添加元素
hashmap通过put(K key, V value)方法添加数据,通过取余运算获取该元素要添加到数组的那个位置,如果已经是树了就直接添加到树里 否则再判断链表大小是否大于8来树化链表。
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
/**
* Implements Map.put and related methods
*
* @param hash hash for key
* @param key the key
* @param value the value to put
* @param onlyIfAbsent if true, don't change existing value
* @param evict if false, the table is in creation mode.
* @return previous value, or null if none
*/
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)//判断节点数组是不是null 创建node数组
n = (tab = resize()).length;
//(n - 1) & hash 取余
if ((p = tab[i = (n - 1) & hash]) == null)//该key在数组中的位置是null 则创建新节点
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))//如果他们key的hash值和key都相等 则替换为新的节点
e = p;
else if (p instanceof TreeNode) //判断是否已经是红黑树
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st 判断是否大于8 需要树化
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))//如果他们key的hash值和key都相等 则替换为新的节点
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
TreeNode<K,V> replacementTreeNode(Node<K,V> p, Node<K,V> next) {
return new TreeNode<>(p.hash, p.key, p.value, next);
}
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
//判断链表是否为null或者链表长度小于最小树化容量
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();//扩容
else if ((e = tab[index = (n - 1) & hash]) != null) {//数组位置不是null
TreeNode<K,V> hd = null, tl = null;
do {//循环链表
TreeNode<K,V> p = replacementTreeNode(e, null); //创建新树节点
if (tl == null)//表头?
hd = p;
else {
p.prev = tl;//双向链表?
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
hd.treeify(tab);//树化
}
}